On I-SVD
Our laboratory continually develops numerical computation package LAPIS (Linear Algebra Package by Integrable Systems) which is based on integrable systems. In this web page, we show a summary of the singular value decomposition algorithm I-SVD which plays a key role in LAPIS.
- Background (singular value decomposition)
- Singular value computation library DLVS
- Singular value decomposition code DBDSLV
- A characteristic of the I-SVD method
- Developer members
Background (singular value decomposition)
Singular value decomposition is widely applied to information retrieval, image processing, least squares problem, and so on. As an open code of singular value decomposition for a bidiagonal matrix implemented in a standard package library LAPACK developed in USA, there exist DBDSQR based on the QR algorithm, DBDSDC based on the divide and conquer (DC) method, and DSTEBZ and DSTEIN based on the bisection and the inverse iteration methods. As an open code of singular value computation for a bidiagonal matrix, DLASQ based on the dqds algorithm is implemented in LAPACK. However, these codes have problem in execution time or precision or reliability. Therefore, we have established a new method for singular value decomposition and plan to open the following code in LAPIS.
Singular value computation library DLVS
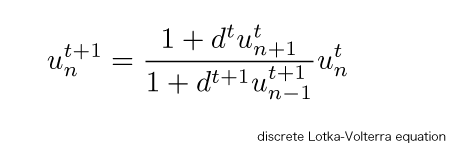
In this project, we present a new algorithm for singular value computation derived from the discrete Lotka-Volterra system. This algorithm is named the mdLVs (modified dLV with shift) algorithm. Similarly to the dqds algorithm, the mdLVs algorithm can be expressed in a form of the LR method with shift. While, shift of origin introduced to the mdLVs algorithm is based on mathematical principles which is different from that in the dqds algorithm. This shift of origin gives high reliability of local exponential stability to the mdLVs algorithm. The mdLVs algorithm is implemented in code DLVS. In this code, shift is estimated thorough the generalized Newton shift which is originally developed in our laboratory. We have recognized that DLVS code achieves high accuracy next to DSTEBZ code and fast execution time next to DLASQ by numerical experiment with large matrices generated from random numbers. Thus, we have succeeded to develop DLVS code which is well-balanced in all execution time, precision and reliability. This library consists of several routines for computation of singular values with the above-mentioned method.
| algorithm | the QRs algorithm | the DC algorithm | the dqds algorithm | the bisection method | the mdLVs algorithm |
|---|---|---|---|---|---|
| code | DBDSQR | DBDSDC | DLASQ | DSTEBZ | DLVS |
| execution time, computational cost | △ | ○ or △ | ○ | × | ○ |
| relative accuracy | × | × | ○ | ○ | ○ |
| reliability | ○ | △ | △ | ○ | ○ |
Singular value decomposition code DBDSLV
In this project, we develop singular value decomposition named the I-SVD (Integrable-Singular Value Decomposition) method based on a new conception. The I-SVD method consists of two parts. One is for singular value computation with the mdLVs algorithm and the other is for singular vector computation with the dLV-type twisted factorization, respectively. In an international standard code library LAPACK, two types of practical singular value decomposition codes are opened. The one is DBDSQR code. In this code, the Demmel-Kahan QR method (1991, SIAM SIAG/LA Prize), which computes singular values and singular vectors of an upper bidiagonal matrix simultaneously by the QR method with shift, is implemented. This code is widely utilized in software packages, such as MATLAB. However, this code has the following defects. Relative accuracy of computed singular values are not guaranteed. Accuracy of computed singular vectors is not sufficient except orthogonality. Computational cost, which is the most important problem, for complete execution of this code is $O(N^3)$. As an algorithm which makes up for low computational speed of the Demmel-Kahan QR method, there exists the Divide & Conquer (DC) method(1997, SIAM SIAG/LA Prize) . This algorithm divides an upper bidiagonal matrix into $25\times 25$ block matrices. Then, singular values and singular vectors of these block matrices are computed by the QR method and stored in memories. Finally, singular vectors of the input matrix are obtained from these results. A code which the DC method is implemented is called DBDSDC. Relative precision of singular values obtained by this method is not good. Especially, small singular values is not computed with high relative precision. For a matrix its singular values are relatively close, the DC method can execute singular value decomposition with $O(N^2)$ computational cost. On the other hand, for a matrix its singular values are relatively dispersed, the DC method is an $O(N^3)$ algorithm similarly to the QR method.
In our project, we have developed a code DBDSLV of the I-SVD method. In singular value computation part of this code, the DLVS code of the mdLVs method is implemented. In singular vector computation part of this code, the dLV-type twisted factorization is implemented. Singular values can be computed fastly with $O(N^2)$ computational cost with the mdLVs method. Even if a singular value is small, it can be computed with high relative accuracy. In singular vector computation, they can be fastly computed with $O(N^2)$ computational cost with the dLV-type twisted factorization. Therefore, we have developed singular value decomposition code with $O(N^2)$ computational cost for whole computation. This computation is very fast. Computation of singular vectors which correspond to a clustered singular values has difficulty. The DBDSLV code improves orthogonality of such singular vectors by the inverse iteration method and the Gram-Schmidt method, if it is necessary. Computational cost for such a matrix by the DBDSLV code is $O(N^2+NK^2)$, where $K$ is cluster size.
Characteristics of the I-SVD method
The dLV-type twisted factorization, which is the core part of the I-SVD method, is a method to compute the Cholesky decomposition of an ill-conditioned symmetric tridiagonal matrix to each singular value which is computed by the mdLVs method with high relative accuracy with high speed and high accuracy in $O(N)$ computational cost. An example where the Cholesky decomposition of a matrix with high accuracy in spite of failure with the qd-type twisted factorization (SIAM SIAG/LA Prize, 2006) is known. See "可積分系の機能数理 (Kasekibunkei no Kinou-Suuri)" by Nakamura, Kyoritsu Shuppan Co., Ltd., 2006. Since singular vector computation part of this method is suited to parallel computing, further fast computing is possible. Orthogonality of singular vectors computed by the I-SVD method without the Gram-Schmidt method is inferior to the Demmel-Kahan and the DC methods which utilize similarity transformation by orthogonal matrices. However, in accuracy of computed singular vectors itself, the I-SVD method is superior the Demmel-Kahan and the DC methods. Therefore, the I-SVD method is suitable for computation which requires singular vectors with high accuracy. For problems which orthogonality of singular vectors is important, the I-SVD method utilizes the Gram-Schmidt method as supplements.
| algorithm | QR | DC | I-SVD |
|---|---|---|---|
| code | DBDSQR | DBDSDC | DBDSLV |
| convergence | ○ | △ | ○ |
| speed and computational cost | × | ○ or △ | ○ |
| accuracy of vector | × | × | ○ |
| orthogonality of vectors | ○ | ○ | △ |
| used memories | ○ | × | ○ |
All the codes DBDSLV, DBDSQR and DBDSDC are singular value decomposition codes for a bidiagonal matrix. Therefore, in singular value decomposition of dense matrix, transform to a bidiagonal matrix by the Householder transform as pre-processing and inverse transform as pros-processing are necessary. By the I-SVD method, execution time of singular value decomposition part of a bidiagonal matrix becomes much shorter. Then, for users of the DBDSLV code, pre-processing and post-processing takes much longer time than singular value decomposition part of a bidiagonal matrix. Therefore, we work on decrease of execution time of whole the I-SVD method actively. In our work, decrease of execution time of pre-processing and post-processing in parallel computing environment such as BLAS (Basic Linear Algebra Subprograms), supercomputer, PC cluster, multi-/many-core, GPU and so on is included.
Development members
- Research director
- Yoshimasa Nakamura
- Research members (in JFY 2012)
- Kimji Kimura,Takumi Yamashita and Hiroki Toyokawa.
- Research collaborators
- Masashi Iwasaki (Kyoto Prefectural University),Masami Takata (Nara Woman's University), Yusaku Yamamoto (Kobe University) and Satoshi Tsujimoto (Kyoto University)
- OB
- Yosuke Iwama,Masahiko Obata,Hiroaki Aida,Atsushi Kobayashi,Shinya Kobayashi,Satoshi Takayama,Yukio Matsui, Hiroyuki Matsuda, Tetsuyoshi Yamamoto,Yukitaka Minesaki,Tatsuya Ishikawa,Hiroaki Tsuboi,Wang Tang, Motoki Katayama,Kenichi Yadani,Taro Konda, Akira Ajisaka and Munehiro Nagata
