I-SVDについて
本研究室では,可積分系による数値計算パッケージ LAPIS (Linear Algebra Package by Integrable Systems) の開発を継続的に行っております.このページでは,LAPISの中心的な位置を占める特異値分解アルゴリズム: I-SVDについて,その概要を述べます.
研究背景 (特異値分解)
特異値分解は,情報検索,画像処理,最小2乗問題等に広く用いられています.アメリカの標準パッケージライブラリLAPACKにおいて公開されている2重対角行列の特異値分解コードとしてはQR法に基づくDBDSQR,分割統治法DCに基づくDBDSDC,2分法と逆反復法に基づくDSTEBZ,DSTEINがあります.また,特異値計算コードとしてはdqds法によるDLASQがあります.しかし,これらのコードは,速度・精度・信頼性のどれかに問題が指摘されています.そこで,我々は,新たな特異値分解法を確立し,LAPISにおいて以下の実装コードの公開を予定しています.
特異値計算ライブラリ DLVS
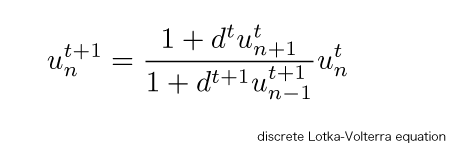
本プロジェクトでは,dLV (離散ロトカ・ボルテラ: discrete Lotka-Volterra) 系を用いて,新たな特異値計算法 mdLVs (modified dLV with shift) を提案しています.このアルゴリズムはdqds法と同じくシフトつきLR法の形に書くことができますが,dqds法とは異なる数学的原理に基づく原点シフトが導入されており,局所的指数関数的安定性という高い信頼性をもつことが示されています.なお,mdLVs法を実装したDLVSコードでは,原点シフト量の設定にこれも独自開発の一般化ニュートンシフトを採用しています.ランダムに生成した大規模行列についての数値実験で,DLVSコードはDSTEBZに次ぐ高い相対精度,DLASQに次ぐ高速性をもつことが確認されています.この結果,精度,速度,信頼性のすべてにバランスのとれたDLVSコードの開発に成功しました.本ライブラリは,この計算法を用いて特異値を計算するいくつかのルーチンによって構成されています.
| アルゴリズム | QRs法 | DC法 | dqds法 | 2分法 | mdLVs法 |
|---|---|---|---|---|---|
| コード | DBDSQR | DBDSDC | DLASQ | DSTEBZ | DLVS |
| 速度・計算量 | △ | ○ or △ | ○ | × | ○ |
| 相対精度 | × | × | ○ | ○ | ○ |
| 信頼性 | ○ | △ | △ | ○ | ○ |
特異値分解コード DBDSLV
本プロジェクトでは,さらに,新構想の特異値分解法 I-SVD (Integrable-Singular Value Decomposition) を開発しています.I-SVD法では,行列の特異値分解を特異値計算部と特異ベクトル計算部に分け,それぞれ,mdLVs法とdLV型ツイスト分解法により計算します.国際標準コードライブラリのLAPACKでは,2種類の実用的な特異値分解コードが公開されています.ひとつはシフトつきQR法によって上2重対角行列の特異値と特異ベクトルを同時に計算するDemmel-Kahan QR法 (1991, SIAM SIAG/LA Prize) を実装したDBDSQRです.これはMATLABなどの汎用ソフトウェアにおいて広く使われています.しかし,特異値の相対精度が保証されず,直交性を除いて特異ベクトルの精度も十分でなく,何より全体では $O(N^3)$ の計算量を必要とする欠点があります.Demmel-Kahan QR法の低速性を補ったアルゴリズムにDivide & Conquer (DC) 法(1997, SIAM SIAG/LA Prize) があります.これは上2重対角行列を $25\times 25$ のブロック行列に分割した上でQR法を適用して特異値特異ベクトルを計算し,メモリに蓄えておいて,後で全体の特異ベクトルに統合するもので,その実装コードはDBDSDCと呼ばれます.しかし,特異値の相対精度が悪く,小さな特異値は精度良く求まりません.特異値が近接する行列では $O(N^2)$ の計算量で高速に特異値分解できるのに対して,特異値の散らばりの大きな行列では,QR法と同じく $O(N^3)$ のアルゴリズムとなってしまいます.
これに対して,本プロジェクトでは,特異値計算部にmdLVs法を実装したDLVSを組み込み,dLV型ツイスト分解法による特異ベクトル計算部を付加することでI-SVD法の実装コードDBDSLVを開発しました.特異値計算には,mdLVs法によって $O(N^2)$ の計算量で高速かつ小さな特異値も高い相対精度で特異値に計算することができます.特異ベクトル計算では,dLV型ツイスト分解によって $O(N^2)$ の計算量で高速に特異ベクトルを求めます.全体を通じて $O(N^2)$ の計算量の極めて高速な特異値分解コードが完成しました.なお,特異値・特異ベクトル分離型の特異値分解で問題となる近接する特異値に対する特異ベクトル計算では,DBDSLVでは必要とあれば逆反復法とグラム・シュミット法により特異ベクトルの直交性を改善します.近接特異値のなすクラスタの大きさを $K$ とすれば,このような行列に対するDBDSLVの計算量は $O(N^2+NK^2)$ となります.
I-SVD法の特徴
I-SVD法の心臓部であるdLV型ツイスト分解法は,mdLVs法によって高い相対精度をもって計算された特異値のひとつひとつに対して,対称3重対角行列の悪条件のコレスキー分解を $O(N)$ の計算量で高速・高精度に計算する手法です.同種のdq型ツイスト分解(2006年 SIAM SIAG/LA Prize) が破綻する場合でも高精度なコレスキー分解が得られる例が知られています.中村著「可積分系の機能数理」(2006年,共立出版)参照.また,特異ベクトル計算部の並列性が高いことから並列化による一層の高速化が可能です.また,I-SVD法によって計算された特異ベクトルは,グラム・シュミット法による直交性の改善なしでは,直交行列による相似変換を利用したDemmel-Kahan法,DC法には直交性で及ばないものの,ベクトル自身の精度ではむしろI-SVD法が優れており,高精度な特異ベクトルが必要とされる実問題に適しています.直交性が特に重視される問題ではグラム・シュミット法を補助的に用います.
| アルゴリズム | QR法 | DC法 | I-SVD法 |
|---|---|---|---|
| コード | DBDSQR | DBDSDC | DBDSLV |
| 収束性 | ○ | △ | ○ |
| 速度・計算量 | × | ○ or △ | ○ |
| ベクトルの精度 | × | × | ○ |
| ベクトルの直交性 | ○ | ○ | △ |
| メモリ使用量 | ○ | × | ○ |
なお,DBDSLV, DBDSQR, DBDSDCはいずれも2重対角行列の特異値分解コードであるため,与えられた密行列の特異値分解には,前処理としてハウスホルダー変換による2重対角化と後処理の逆変換が必要です.I-SVD法の登場により2重対角行列の特異値分解部が非常に高速化されたため,DBDSLVのユーザにとっては前処理と逆変換が特異値分解の計算時間の大部分を占めるようになってしまいました.そこで,本プロジェクトでは,BLAS (Basic Linear Algebra Subprograms) やスパコン,PCクラスタ,マルチコア/メニーコア,GPU等の並列計算機環境における前処理と逆変換の高速化を含むI-SVD法の全体の一層高速化についても積極的に取り組んでいます.
開発メンバー
- 研究代表者
- 中村佳正
- 研究参加者 (2012年度)
- 木村欣司,山下巧,豊川博己
- 研究協力者
- 岩崎雅史 (京都府立大学),高田雅美 (奈良女子大学),山本有作 (神戸大学),辻本諭 (京都大学)
- OB
- 岩間陽介,小幡雅彦,合田紘章,小林篤史,阪野真也,高山智史,松井佑貴夫,松田浩幸,山本哲由,峯崎征隆,石川達也,坪井洋明,王坦,片山幹基,矢谷健一,誉田太朗, 鯵坂明,永田宗寛
