研究内容・研究活動
「応用可積分系」をキーワードに幅広い研究を行っています.
- 研究室紹介資料 2015 (PDF): 2015年4月の情報学科 (学部) 生向け分野配属説明会で使用した資料です.
応用可積分系: Applied Integrable Systems
「可積分系」とは,古典力学においては Liouville-Arnold の意味で完全積分可能な系,すなわち自由度と同じ数の独立な保存量を持ち,解を具体的に書き下すことができる非線形力学系のことを指します.単振子やコマなどが可積分系として古くから知られていましたが,20世紀に入って KdV 方程式 (浅い水面を伝わる波のモデル,ソリトンと呼ばれる) や戸田格子と呼ばれる新たに発見された可積分系の研究が盛んに行われるようになりました.これらが古典的な可積分系と異なるのは,自由度も保存量も無限個あるということであり,非線形系でありながら著しい性質を示すことが知られています.
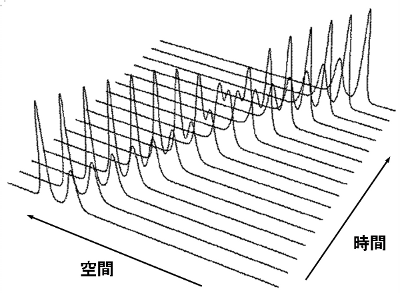
ソリトンの追い越し
可積分系の研究が進展した20世紀は,計算機が飛躍的な発展を遂げた時代でもありました.計算機では数値は離散値 (飛び飛びの値) をとり,連続量を扱うことはできません.このため,計算機上で力学系を扱うためには,時間・空間の離散化が重要な課題となります.可積分系については,その解の構造を保つような「よい」離散化が可能であることが経験的に知られており,厳密な定義はありませんが,このようにして離散化された系を離散可積分系と呼んでいます.
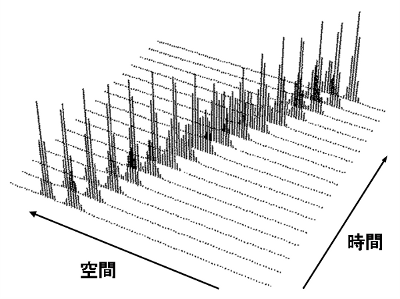
離散ソリトンの追い越し
1990年代以降,この離散可積分系とある種の数値計算アルゴリズムの間に密接な関係が見出され,可積分系と数値解析の境界上での研究が飛躍的に発展しました.また,最近は従属変数をも離散化した超離散可積分系と呼ばれるものを用いた種々の現象の数理モデル化も試みられています.我々はこのようにして誕生した「応用可積分系」を中心的なテーマに据え,数学の理論から計算機上でのアルゴリズムの実装まで,多岐に渡る研究を行っています.
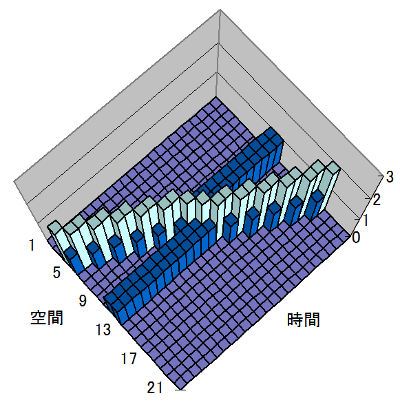
超離散ソリトンの追い越し
キーワード
漸化式,オートマトン,直交多項式,計算アルゴリズム,超幾何関数,離散/超離散可積分系,箱玉系,双線形化法,連分数,Padé 近似,戸田格子,Lotka-Volterra 方程式,行列特異値計算/分解,収束加速法,…….
主な研究テーマ
直交多項式に基づく可積分系の応用解析の研究
離散可積分系と直交関数系の密接な関わりを研究の足掛りとして,両者の持つ数学的構造を解明していきます.また,得られた結果の工学への応用を考えます.
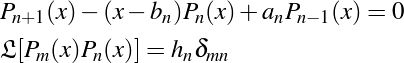
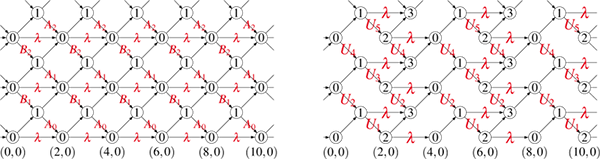
- 直交関数系のスペクトル変換と離散可積分系
- 離散可積分系の特殊関数 (超幾何) 解の探求
- 離散可積分系のグラフによる組合せ論的解釈
- 新しい直交関数系の探索とその応用
箱玉系のルールとその解析
高橋・薩摩による箱玉系の有限オートマトン表示に対する考察の中から, “箱飛ばしルール”や“空箱ルール”などを導入した新しい箱玉系に関する研究を行なっています.
離散可積分系に基づく新しい計算アルゴリズムの開発
離散可積分系の理論を用いることで様々な計算アルゴリズムの開発が可能です.
- 離散戸田格子の理論を発展させることで,一般化固有値問題の新しい計算アルゴリズムの定式化が可能です.
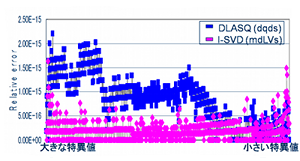
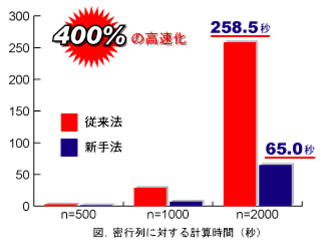
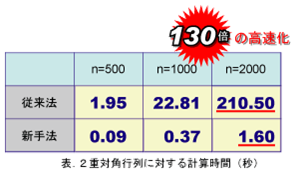
- 離散 Lotka-Volterra 方程式をベースとして定式化された行列の特異値計算アルゴリズムが,特異ベクトル計算部も加えた I-SVD への開発と繋がりました.I-SVDと従来法の比較は以下のとおりです.

アクティビティ
- 日本応用数理学会「応用可積分系」研究部会
- 関西可積分系セミナー (KISS),計算数学研究会
- JSPS科研費挑戦的萌芽研究 2016 – 2019
- JSPS科研費基盤研究(B) 2019 – 2024
- JSIAM Letters
普段の活動については,現役学生による研究室紹介も合わせてお読み下さい.

